1. 통계와 수학
고유값과 고유벡터란?
-
선형대수학에서 주어진 정방행렬(row, col의 수가 같은)
가 있을 때, 어떤 0이 아닌 벡터 에 대해
를 만족하는 스칼라와 벡터 를 각각 고유값, 고유벡터라고 한다 따라서
가 선형변환을 나타낸다고 할 수 있고 이때 고유벡터는 선형변환 에 의해 '방향은 그대로 유지하면서' 길이만 변하는 벡터이다 어떤 벡터
가 고유벡터라는 것은 는 에 의해 변환되더라도 고유한 방향을 잃지 않는 다는 것을 의미한다. 고유값과 고유벡터는 선형변환(또는 행렬)의 가장 중요한 특징 중 하나로, 변환이 벡터에 미치는 영향을 ‘축 방향(고유벡터)’과 그 ‘크기 변화 비율(고유값)’로 파악할 수 있게 해 줍니다.
- 고유값
는 이라는 특성방정식을 통해 구합니다. - 특정
에 대한 고유벡터는 를 풀어서 구합니다.
이러한 고유값과 고유벡터는 PCA와 같은 기술에서 활용됩니다.
- 고유값
샘플링(Sampling)과 리샘플링(Resampling)이란?
-
샘플링: 표본추출을 한다는 의미, 모집단 전체에 대한 추정치를 얻기 위해 임의의 sample을 선택
모집단을 전부 조사할 수 없을 때 사용하며 모집단 전체와 비슷하지만 완전히 동일하다고는 볼 수 없다. = noise가 존재할 수 밖에 없다. -
리샘플링: 모집단의 분포형태를 알 수 없을 때 주로 사용하는 방법,
현재 가지고 있는 데이터를 통해 모집단의 분포와 가장 비슷한 분포를 만들자! 라는 개념
가지고 있는 샘플에서 다시 샘플을 추출 하여 통계량의 변동성을 확인, 즉 샘플링을 여러번 반복하는 방법
K-Fold 교차 검증이 대표적인 예시표본을 추출하면서 원래 데이터 셋을 복원하기 떄문에 이를 통해서 모집단의 분포에 어떤 가정도 필요없이 표본만으로 추론이 가능하다는 장점이 있다.
확률 모형과 확률 변수란?
-
확률변수: 표본 공간의 각 단위 사건에 실수 값을 부여하는 변수, 특정 확률로 발생하는 각각의 결과를 수치적 값으로 표현하는 변수라고 할 수 있다
이산 확률 변수, 연속 확률 변수 두가지의 경우로 나눌 수 있다- 이산 확률 변수: 확률 변수
가 취할 수 있는 값이 유한하기 때문에 셀 수 있는 확률 변수 - 연속 확률 변수: 어떤 두 수 사이에 반드시 다른 수가 존재하는, 셀 수 없는 범위의 확률변수를 가지는 경우
일단 주사위를 굴리는 상황은 어떤 수가 나올지 모르므로, 확률상황이다. "주사위를 굴렸을 때 나오는 값"을 확률변수 X라고 할 수 있다.1~6이 표본공간이 되고, 셀 수 있으므로 이산확률변수가 된다.P(X=1)와 같은 식으로 표현하고, 이는 "주사위를 굴렸을 때, 1이라는 값이 나올 확률"로 해석할 수 있다. - 이산 확률 변수: 확률 변수
-
확률 모형: 확률 변수를 이용하여 데이터의 분포를 수학적으로 정의한 모형,
데이터의 분포를 묘사하기 위해 사용, 보통 확률 분포 함수 or 확률 밀도 함수를 주로 사용한다.
이때 함수의 계수를 분포의 모수(Parameter)라고 부른다.
확률 분포는 표본공간에서 정의된 확률을 이용하여 확률을 표현한 것, 대표적인 예시가 가우시안 분포
누적 분포 함수와 확률 밀도 함수의 정의와 수식
-
확률 변수 X가 임의의 실수 집합 B에 포함되는 사건의 확률이 다음과 같이 어떤 음이 아닌 함수 f의 적분으로 주어진다고 하자.
이 때의 X를 연속확률변수라고 하며, 함수 f(x)를 **확률 밀도 함수(Probability Density Function, PDF)**라고 한다. 단, 실수 집합 B가 실수 전체일 경우 실수 전체에 대한 확률밀도함수의 적분은 1을 만족해야 한다.
**누적 분포 함수(Cumulative Distribution Function, CDF)**는 확률변수가 특정 값보다 작거나 같을 확률을 나타내는 함수이다. 특정 값을 a라고 할 때, 누적 분포 함수는 다음과 같이 나타낼 수 있다.
확률 밀도 함수와 누적 분포 함수는 미분과 적분의 관계를 갖는다. 확률 밀도 함수를 음의 무한대에서 특정값 a까지 적분을 하면, a에 대한 누적 분포 함수를 얻을 수 있다. 반대로 누적 분포 함수를 미분하면 확률 밀도 함수를 얻을 수 있다.
조건부 확률
-
정의: 사건
가 일어났다는 전제 하에 사건 가 일어날 확률, 로 표현 가능
이는 베이즈 정리와도 이어진다. -
베이즈 정리
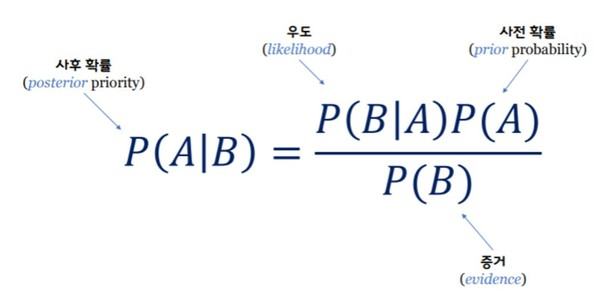
- 변수 설명
B: 새로 관찰되는 데이터
A: 모델에서 계산하고 싶어하는 모수 (가설)
사후확률(Posterior): 데이터를 관찰했을 때, 이 가설이 성립할 확률 (데이터 관찰 이후 측정하기 때문에 사후확률)
사전확률(Prior): 가설에 대해 사전에 세운 확률 (데이터 관측 이후 사후확률이 사전확률이 된다.)
가능도(Likelihood): 현재 주어진 모수 (가정) 에서 이 데이터가 관찰될 가능성
증거(Evidence): 데이터 전체의 분포
- 변수 설명
공분산과 상관계수
-
공분산: 확률변수
와 평균의 차이와 확률변수 와 평균의 차이를 곱한 것의 평균값 두 변수 간에 양의 상관관계가 있는지, 음의 상관관계가 있는지 정도를 알 수 있다. 하지만 그 상관관계가 얼마나 큰지는 제대로 반영하지 못한다.
문제점: 확률변수의 단위 크기에 영향을 많이 받는다.
→ 상관계수를 사용 -
상관 계수: 확률변수의 절대적 크기에 영향을 받지 않도록 공분산을 단위화, 즉 공분산에 각 확률변수의 분산을 나눈다
상관계수는 양의 상관관계가 있는지 음의 상관관계가 있는지 알려줄 뿐만 아니라, 그 상관성이 얼마나 큰지도 알려준다.
1에 가까울 수록 크고 0에 가까울 수로 작다.
신뢰 구간
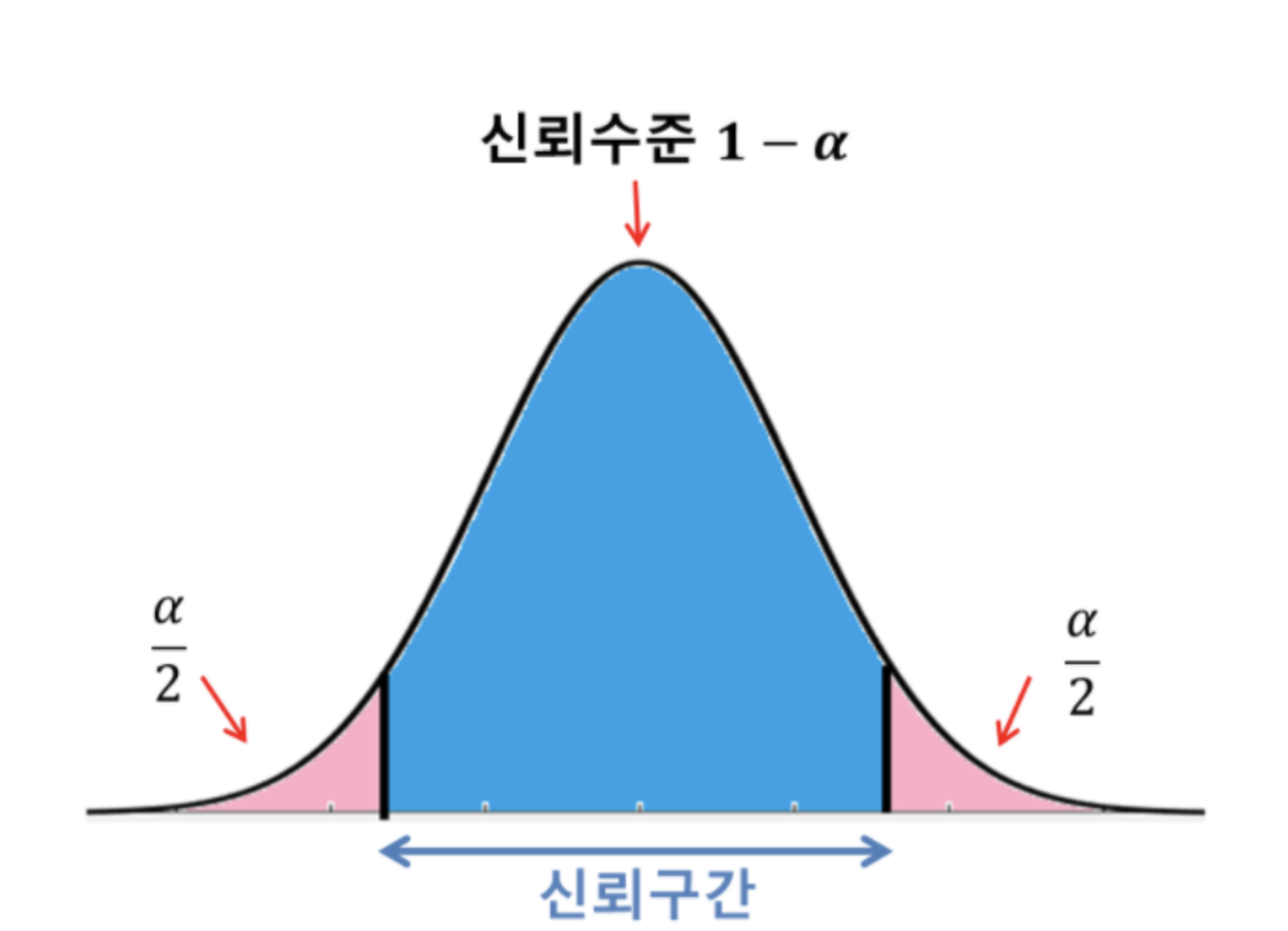
- 정의: 모집단의 모수가 위치해 있을 것으로 신뢰할 수 있는 구간
신뢰구간을 구하는 이유는 모수의 신뢰성을 가늠하기 위해서이다.
95% 신뢰구간이로 주어졌다고 했을 때, 이는 “많은 표본을 반복 추출하여 동일한 방식으로 95% 신뢰구간을 구하면, 그 중 95%가 실제 모집단의 모수를 포함하게 된다” 라는 의미이다.
모집단: 연구나 조사에서 관심 있는 전체 대상 집합을 의미
모수: 모집단의 평균, 분산, 비율 등이 모수에 해당
P-value
-
p-value를 알기 위해서는 먼저 1종 오류를 알아야 한다. 여기서 1종 오류란 귀무가설이 참인데 기각한 경우을 말한다. 귀무가설이란 기존의 주장을 말하며, 이와 반대로 새로운 주장을 대립가설이라고 한다.
예를 들어, 어느 제약회사에서 치료약 A를 개발했다. 기존에는 치료약 A가 없었으므로 귀무가설은 "치료약 A가 효과가 없다"라고 설정한다. 반대로 대립가설은 "치료약 A는 효과가 있다"로 설정한다. 회사에서는 검정을 한 결과, 귀무가설을 기각하고 대립가설을 채택했다. 치료약 A는 판매되었고 높은 매출을 기록했다. 그런데 알고보니 치료약 A가 효과가 없다는 것이 밝혀졌다. 참인 귀무가설을 기각했기에 이는 1종 오류가 일어났다고 볼 수 있다.
다시 돌아와서 p-value는 1종 오류를 범할 확률을 말한다. 예를 들어, p-value가 5%라면, 100번 중 5번 1종 오류가 발생한다는 말이다. 검정을 할 때는 유의 수준 α를 정하는데, 이것이 1종 오류의 상한선이 된다. 그래서 유의 수준보다 p-value가 작다면 실험의 오류가 상한선보다 작으므로 귀무가설을 기각하고 대립가설을 채택한다. 만약 크다면 상한선을 넘었으므로 귀무가설을 채택한다.
R square의 의미
-
결정 계수(R square)는 선형 회귀 모델에서 데이터에 대해 회귀선이 얼마나 잘 설명하는지에 대한 설명력을 의미
결정계수는 0~1의 값을 가질 수 있고, 만약 값이 1이라면 회귀선으로 모든 데이터를 다 설명할 수 있다고 이해할 수 있다. 반대로 0에 가까울수록 설명력이 거의 없음을 의미한다.결정계수는 다음의 식으로 구할 수 있다.
-
-
-
이외에도 MAE, MSE, RMSE등이 있다. -
주의사항
- (독립)변수 수가 늘어나게 되면
는 보통 증가하게 된다. - 변수가 무작정 많아져
를 높일 수 있어 과적합 가능성이 존재한다. 이 높다고 해서 인과관계가 성립한다고는 할 수 없다. - 단순 선형 회귀에서만 사용가능하다.
- (독립)변수 수가 늘어나게 되면
-
평균(mean)과 중앙값(median)의 사용기준
-
평균(mean): 모든 관측값의 합을 자료의 개수로 나눈 것
전체 관측값(실제값)이 고루 분포되어 있고, 평균 근처에 표본이 몰려 있는 상황에서 대표값으로 유용
이상치와 같은 극단적인 값에 영향을 크게 받는다. -
중앙값(median): 전체 관측값을 크기 순서로 배열했을 때 가운데 위치하는 값
평균과 달리 관측값들의 변화에 민감하지 않고, 이상치와 같은 극단적인 값에 영향을 거의 받지 않는다.
표본의 편차, 왜곡이 심하게 나타나는 경우에 유용하다.
중심극한정리가 유용한 이유
- 정의: 크기가 n인 표본추출(30개 이상)이 무수히 많이 수행되면(최소 100회 이상을 의미), 표본 평균의 분포가 정규분포에 수렴한다는 의미
모집단의 형태가 어떻든지 간에 상관없이 표본 평균의 분포가 정규분포를 따르기 때문에 유용하다.
엔트로피(Entrophy)와, 정보 이득(Information Gain)
-
엔트로피: 주어진 데이터의 혼잡도를 의미, 엔트로피는 아래 수식과 같이 데이터가 어떤 Class에 속할 확률에 대한 기댓값으로 표현할 수 있다.
데이터가 서로 다른 클래스에 있다면? 엔트로피가 높고, 같은 클래스에 있다면? 엔트로피가 낮다.
→ 각각의 데이터가 특정 클래스에 속할 확률이 높고 나머지 클래스에 속할 확률이 낮다면 엔트로피가 낮고, 모든 각각의 클래스에 속할 확률이 비슷하다면 엔트로피는 높다. -
정보이득: 데이터가 어떤 클래스에 속할 확률이 커짐에 따라 정보를 잘 얻게 되는 것을 의미 → 감소되는 엔트로피 양을 의미한다.
의사결정트리는 가지를 칠 때 어떤 데이터를 두 집합으로 나누었을 때 두 집합의 정보이득이 크도록, 엔트로피는 작아지도록 분할을 한다.
모수적 방법론과 비모수적 방법론을 사용하는 경우
“모수(parameter)”란 분포나 모델을 규정짓는 데 필요한 ‘고정된 수의 척도값(평균, 분산 등)’을 뜻함
-
표본의 통계량(평규, 분산, 표준편차 등)을 통해 모집단의 모수(모평균, 모표준편차 등)를 추정하는 방법을 통계적 추론이라 한다.
-
모수적 방법: 모집단이 어떤 분포를 따른다는 가정 하에 통계적 추론을 하는 방법
표본의 수가 30개 이상일 때 중심극한정리에 의해 정규분포를 따르므로 모수적 방법론을 사용한다.분포나 모델 형태를 이미 ‘딱 정해진’ 어떤 식(함수)으로 가정하고, 그 함수를 결정하는 파라미터만을 추정합니다.
-
예시
-
Z-검정
가정: 모집단이 정규분포를 따르며, 모표준편차()가 알려져 있음
주요 파라미터:(모평균), (알려진 모표준편차).
라는 하나의 파라미터만 추정하거나 검정에 집중하며, 분포 형태는 “정규분포”라는 하나의 가정으로 고정됩니다 -
선형회귀
- 가정:
은 정규분포( )로 가정, 독립·등분산 가정. - 주요 파라미터:
, 그리고 오차항의 분산 . - 이 유한 개의 파라미터들만으로 전체 모델을 설명하며, 분포(정규)는 고정되어 있음.
- 가정:
-
-
장점
적은 데이터로도 사용 가능
분포(모델)가 단순하여 추론/해석이 쉽고 빠름 -
단점
가정이 틀리면 결과가 크게 왜곡
복잡한 패턴을 충분히 포착하지 못함
-
-
비모수적 방법론: 모집단의 분포를 가정하지 않고 추론하는 방법
표본의 수가 30개 미만이거나 정규성 검정에서 정규 분포를 따르지 않는다고 증명되는 경우에 사용-
예시
K-NN 분류 회귀: 새로운 관측치를 예측할 때 (모델이 존재하지 않고) 가장 가까운 '데이터'로만 결정
의사결정나무: 트리 분기를 많이하여 데이터 패턴을 복잡하게 학습 가능
스플라인 회귀: 구간별로 다양한 다항식을 이용함 -
장점
복잡한 분포나 관계를 잡을 수 있는 유연성이 큼
데이터가 많을수록 실제 데이터 패턴과 비슷해짐 -
단점
데이터가 적을 때 Overfitting 위험이 크고 성능이 불안정함
계산량이 많아지고 결과 해석이 직관적이지 않음
-
Likelihood(가능도)와 Probability(확률)의 차이
1. 확률 (Probability)
-
정의:
확률은 어떤 사건이 일어날 가능성을 수치로 표현한 것으로, 주어진 **모수(예: 동전이 앞면이 나올 확률 )**에 대해 결과(데이터)가 발생할 확률을 계산합니다. -
예제:
만약 동전이 앞면이 나올 확률라고 미리 알고 있다면, 3번 던져서 앞면이 2번, 뒷면이 1번 나올 확률은 다음과 같이 계산합니다. 여기서는 미리 정해진 값에 기초하여 결과의 확률을 계산합니다.
2. 가능도 (Likelihood)
-
정의:
가능도는 관측된 데이터가 주어졌을 때, 모수가 특정 값일 “가능성” 을 나타내는 함수입니다. 데이터가 고정되어 있고, 모수 의 값에 따라 그 데이터가 나타날 가능성을 평가하는 것입니다.
아무리 충분히 수행해도 어디까지나 추론이기 때문에 가능성의 합이 1이 아닐 수 있다. -
예제:
동전 3번 던져서 실제로 앞면 2번, 뒷면 1번이 나온 결과를 관측했다고 가정해봅니다.
이때 가능도 함수는 모수 에 대한 함수로 표현할 수 있습니다.여기서 는 관측된 결과를 만들어낸 원인으로서 평가 대상이 됩니다. 즉, “어떤 값이 이 결과를 가장 잘 설명하는가?”를 판단할 때 사용합니다.
요약
-
확률: 모수가 주어졌을 때, 특정한 결과(데이터)가 발생할 확률을 계산합니다.
예: 일 때, 3번 던져 앞면 2번 나올 확률은 0.441. -
가능도: 관측된 데이터가 주어졌을 때, 다양한 값들이 얼마나 그 데이터를 잘 설명하는지(가능성) 를 평가하는 함수입니다.
예: 앞면 2번, 뒷면 1번이 나온 데이터를 바탕으로 형태로 평가합니다.
통계에서 사용되는 bootstrap의 의미
-
부트스트랩: 가설검증을 하거나 Metric을 계산하기 전에 random sampling을 적용하는 방법이다.
현재 가진 표본에서 추가적으로 표본을 복원 추출하고 각 표본에 대한 통계량을 다시 계산 → 여러번의 무작위 추출을 통해, 평균의 신뢰구간을 구할 수 있다. -
머신러닝에서의 부트스트랩
- 랜덤 샘플링을 통해 학습 데이터를 늘리는 방법
- 여러 모델을 학습시켜 추론 결과의 평균을 사용하는 방법(=앙상블)
-
복원 추출: 확률을 구할 때, 추출했던 것을 원래대로 돌려놓고 다시 추출하는 방법을 말한다. 리샘플링 기법 중 하나
모수가 매우 적은 케이스의 경우 예측 모델 수립 방법
= 데이터가 적은 경우
-
표본이 매우 적은 경우(30미만): 표본평균의 분포가 정규 분포를 따른다고 가정할 수 없다 → 비모수적 방법을 채택하여 예측 모델을 수립할 수 있다.
-
표본의 크기 30 이상인 경우: 중심극한정리에 의해 30개 이상의 표본이라면 표본 평균이 정규분포를 따른다고 가정할 수 있으므로 모수적 방법론을 사용한다.
Bayesian(베이지안)과 Frequentist(프리퀀티스트)
-
베이지안: 사건의 확률을 바라볼 때, 사전 확률을 미리 염두해두고 사건의 발생에 따라 베이즈 정리로 사후 확률을 구해 다시 사전 확률을 업데이트시킨다.
즉, 베이지안은 과거의 사건이 현재 사건에 영향을 끼친다는 입장을 가지고 있다. -
프리퀀티스트: 확률을 무한번 실험한 결과, 객관적으로 발생하는 현상의 빈도수로 바라본다.
즉, 프리퀀티스트는 현재의 객관적인 확률에 의해서만 사건이 발생한다는 입장을 가지고 있다.
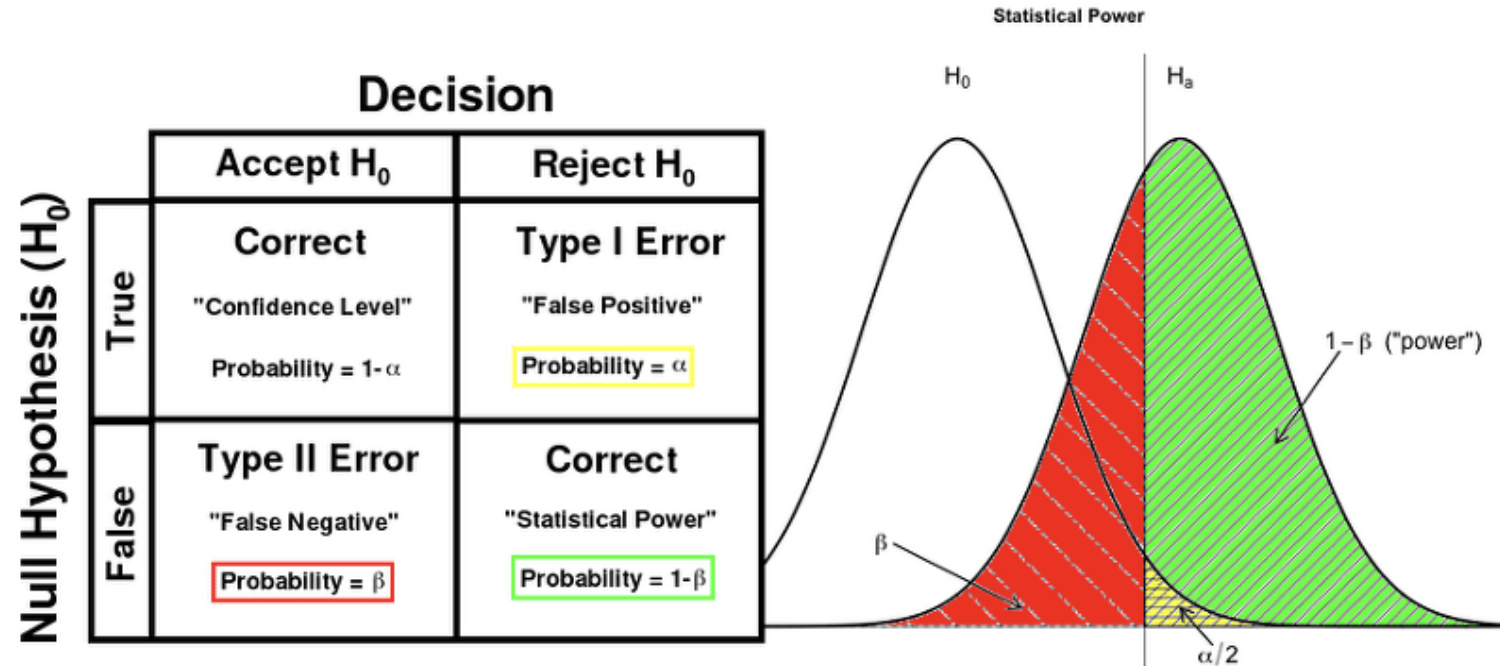
검정력(Statistical power)
| 귀무가설 H0 참 | 귀무가설 H0 거짓 | |
|---|---|---|
| 귀무가설 H0 채택 | 옳은 결정(1-α) | 제 2종 오류(β) |
| 귀무가설 H0 기각 | 제 1종 오류(α) | 옳은 결정(1-β), 검정력 |
- 검정력: 대립가설 H1이 참인 경우 귀무가설 H0를 기각(대립가설 H1을 채택)할 확률이다.
Missing Value가 있을 경우 채울지 말지, 그 이유
-
Missing value를 처리하는 방법
- 그대로 두기: 아무런 처리를 하지 않는다.
- 삭제하기: 누락된 데이터를 제거한다. 이는 중요한 데이터를 잃어버릴 가능성이 존재
- 특정 값으로 채우기: 0, 최빈값, 상수 값으로 채운다.
- 예측하여 채우기: K-means, 평균값, 중앙값으로 채운다.
1번 방법: XGBoost같은 알고리즘은 알아서 결측치를 처리하지만 그러한 로직이 없는 경우에는 오류가 발생하여 학습을 진행할 수 없다 → 결측치는 처리해야한다!
2번 방법: 가장 쉽지만, 중요한 데이터를 잃을 수 있다.
3, 4번 방법: 2번처럼 중요한 데이터를 유지할 수 있지만 결측지가 너무 많다면 채우는 행위 자체가 무의미할 수 있다.
ex) 100개중 99개가 결측치라면..따라서 결측치는 상태, 비율, 모델에 따라 사용할 방법이 달라진다.
이상치를 판단하는 기준
-
이상치: 전체 데이터 패턴에서 벗어난 이상한 값을 의미한다. 이상치는 모델의 성능에 영향을 미치기 떄문에 처리해야한다.
-
탐지 방법
-
IQR(Inter Quantile Range): 데이터를 오름차순으로 정렬하고 25%(
) 50%( ), 75%( )으로 4등분을 한다. - 하한 경계 (Lower Bound):
- 상한 경계 (Upper Bound):
이 경계 밖에 위치하는 데이터 값들을 이상치로 간주합니다.
-
Z-score: 데이터가 평균에서 얼마나 떨어져 있는지를 나타내는 지표로, 임계값을 설정하여 Z-score가 임계값보다 크다면 이상치로 판단한다. 단, 데이터가 가우시안 분포를 따른가는 가정하에 사용해야한다.
-
-
필요한 표본의 크기를 계산하는 방법
-
모집단의 크기
을 구하고, 신뢰수준 와 오차범위 를 얼마로 할지 선정하여 표본의 크기를 구할 수 있다.
신뢰수준은 표본추출을 반복했을 때 얼마나 그 결과를 신뢰할 수 있는지에 대한 정도로 95% 를 주로 사용한다.
오차범위는 작을 수록 모집단의 특성에 대한 유용한 정보를 제공하지만 모집단에 대한 추론이 틀릴 가능성도 높아지므로 10% 를 넘지 않게 한다.
Bias를 통제하는 방법
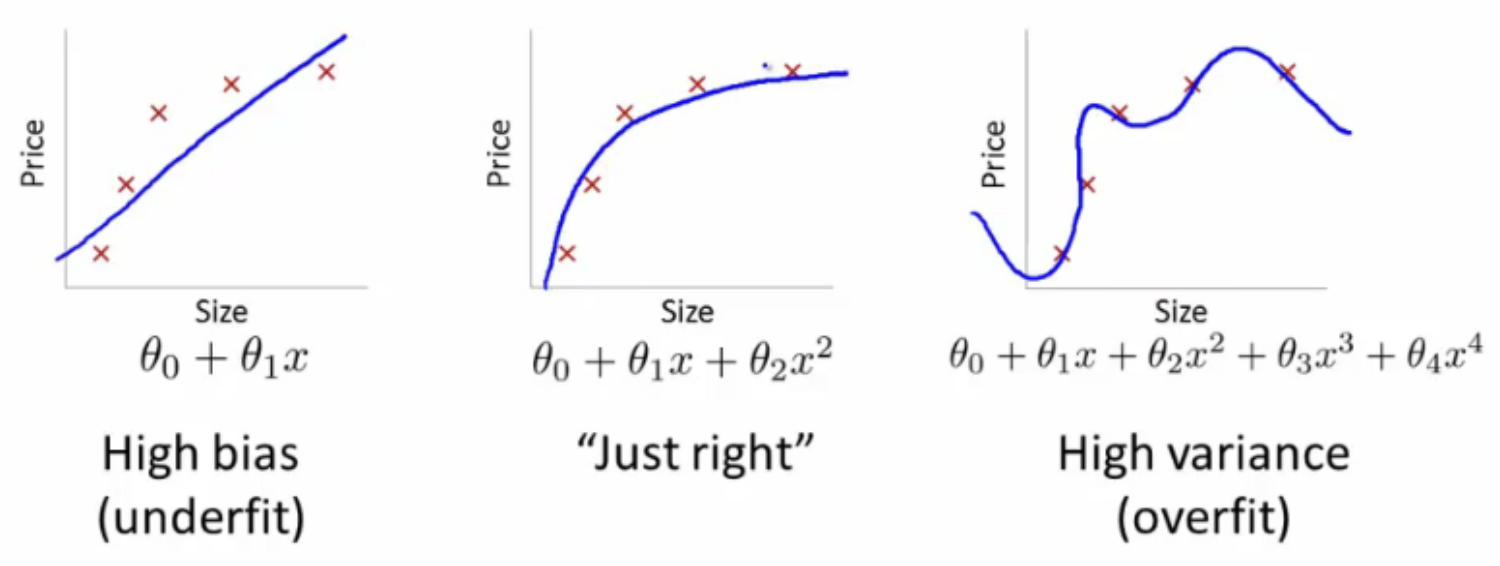
-
Bias(편향): 데이터 내에 있는 모든 정보를 고려하지 않음으로 인해, 지속적으로 잘못된 것들을 학습하는 경향을 의미한다. 이는 언더피팅(Underfitting)과 관계되어 있다.
-
Variance(분산): 데이터 내에 있는 에러나 노이즈까지 잘 잡아내는 highly flexible models에 데이터를 피팅시킴으로써, 실제 현상과 관계 없는 랜덤한 것들까지 학습하는 알고리즘의 경향을 의미한다. 이는 오버피팅(Overfitting)과 관계되어 있다.
-
너무 높은 Bias: 모델이 단순하여 데이터의 중요한 패턴을 놓치게 되고, 이로 인해 underfitting이 발생합니다.
-
너무 높은 Variance: 모델이 학습 데이터에 과도하게 적합되어 새로운 데이터에 대해 일반화 능력이 떨어지게 됩니다.
-
편향과 분산은 한 쪽이 증가하면 다른 한 쪽은 감소하는 Trade-off 관계이다.
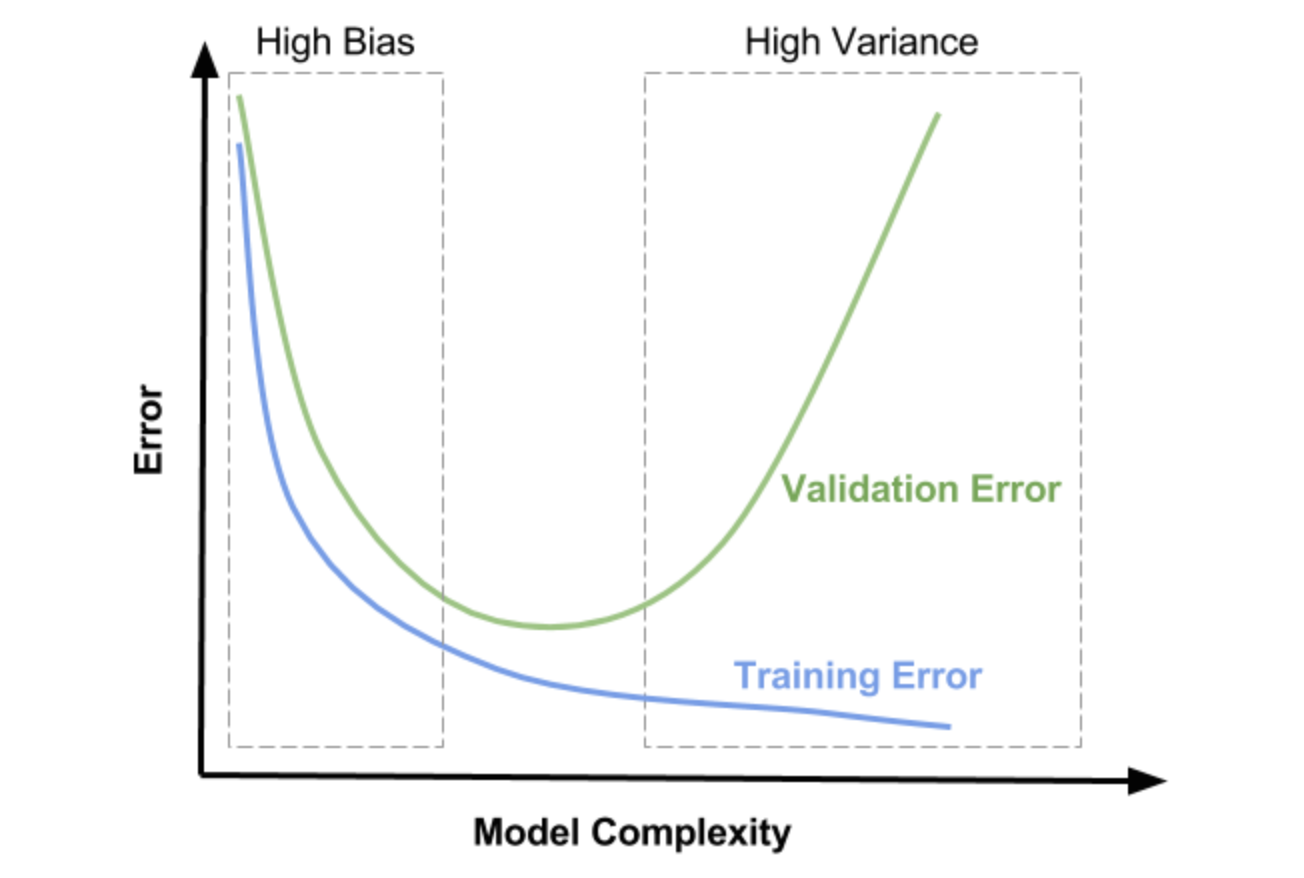
-
Bias를 통제하는 방법
모델 크기 증가
입력 feature 수정
정규화
모델 구조 수정
학습 데이터 추가
로그함수를 사용하는 경우
-
단위 수가 너무 큰 값들을 바로 회귀분석할 경우 결과를 왜곡할 우려가 있어, 이를 방지하기 위해 사용한다.
또한 비선형관계의 데이터를 선형으로 만들기 위해 사용한다.
ex) 제곱 형식의 그래프에 자연로그를 취하면 직선(선형)이 된다. -
로그함수느 0~1사이의 값에서 음수값을 가지므로,
와 같이 처리한다. -
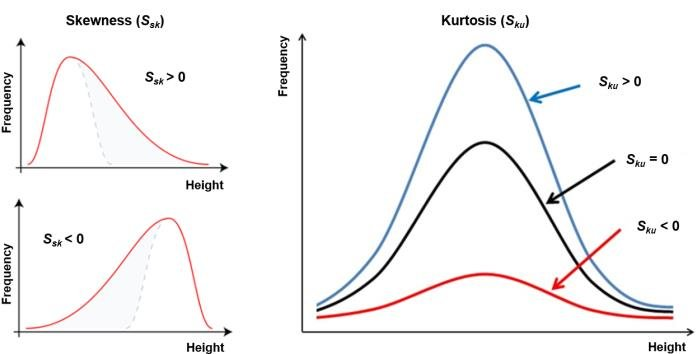
왜도(Skewness)
데이터가 한 쪽으로 치우친 정도이다. -
첨도(Kurtosis)
분포가 얼마나 뾰족한지 나타내는 정도이다.