7. 알고리즘

시간, 공간 복잡도

• 복잡도: 알고리즘의 성능을 평가하는 척도로 **시간 복잡도(Time Complexity)**와 **공간 복잡도(Space Complexity)**로 나뉜다.

  • 시간 복잡도(Time Complexity): 알고리즘에 사용되는 연산 횟수의 총량
  • 공간 복잡도(Space Complexity): 알고리즘에 사용되는 메모리 공간의 총량

  즉, 시간 복잡도는 속도에 대한 분석 결과이고, 공간 복잡도는 메모리 사용량에 대한 분석 결과이다.

• 복잡도 표기법

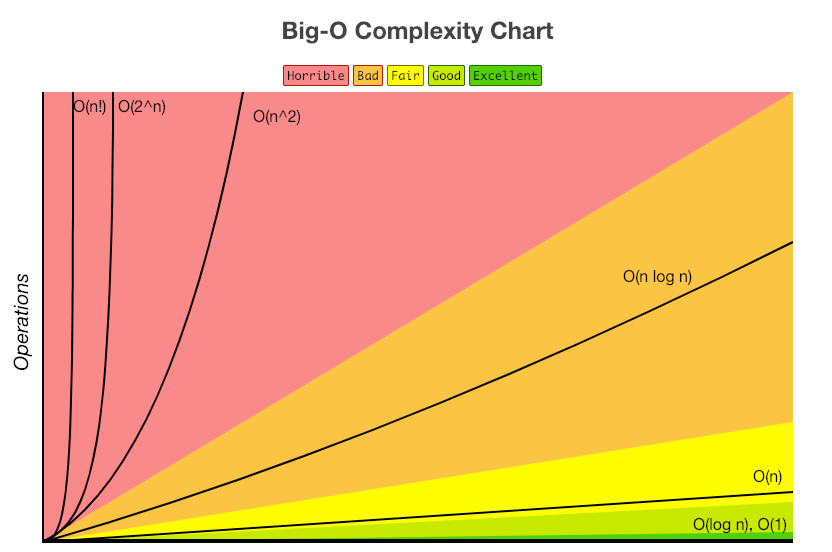
  • O Notation (빅오 표기법): 점근적 상한선 / 최악의 경우
  • Ω Notation (오메가 표기법): 점근적 하한선 / 최상의 경우
  • θ Notation (세타 표기법): 점근적 상한선과 점근적 하한선의 교집합 / 평균의 경우
    

Sort Algorithm

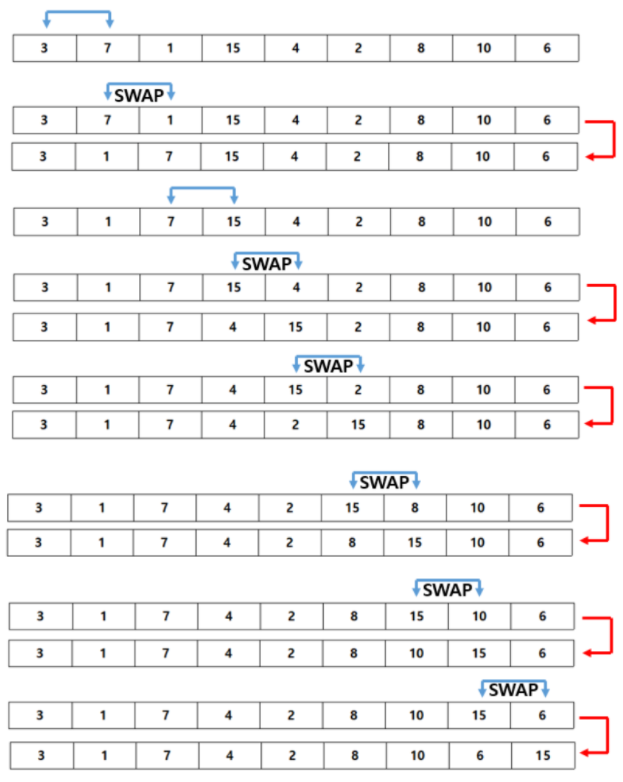
Bubble Sort

• 배열의 0번부터 N-1번까지 탐색을 하면서 인접한 칸과 비교하여 swap을 하는 방식의 정렬 알고리즘이다.
  

• 시간복잡도 $O(N^2)$이다.

• 파이썬 구현

  def bubbleSort(alist):
  for passnum in range(len(alist)-1, 0, -1):
      for i in range(passnum):
          if alist[i] > alist[i+1]:
              temp = alist[i]
              alist[i] = alist[i+1]
              alist[i+1] = temp
  

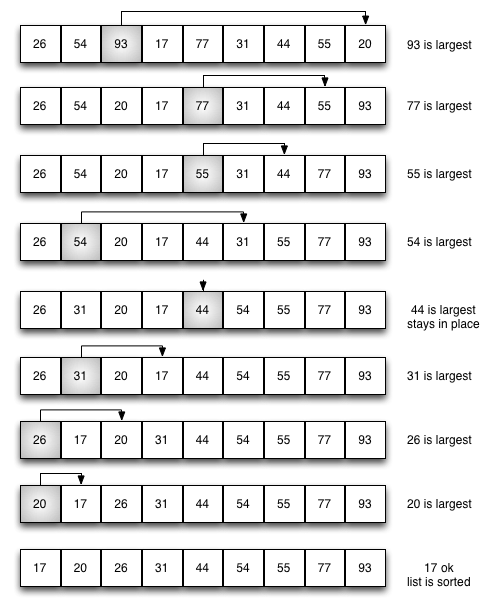
Selection Sort

• 정렬되지 않은 부분에서 최댓값(또는 최솟값)을 찾아 현재 위치의 원소와 교환하는 방식.
• 특징: 비교 횟수는 많지만 swap 횟수는 최소화됨.
• 시간 복잡도: $O(N²)$
• 파이썬 구현

def selectionSort(alist):
    for fillslot in range(len(alist)-1, 0, -1):
        positionOfMax = 0
        for location in range(1, fillslot+1):
            if alist[location] > alist[positionOfMax]:
                positionOfMax = location
        alist[fillslot], alist[positionOfMax] = alist[positionOfMax], alist[fillslot]

Insertion Sort

• 현재까지 정렬된 부분에 새로운 원소를 적절한 위치에 "삽입"하는 방식.
• 시간 복잡도:
  • 최악/평균: $O(N²)$
  • 최선(거의 정렬된 경우): $O(N)$
• 파이썬 구현

def insertion_sort(collection):
    for index in range(1, len(collection)):
        while index > 0 and collection[index] < collection[index - 1]:
            collection[index], collection[index - 1] = collection[index - 1], collection[index]
            index -= 1
    return collection

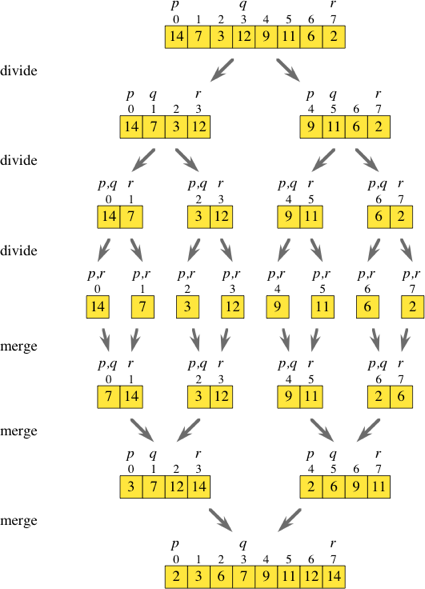
Merge Sort

• Divide & Conquer 방식으로 배열을 반으로 분할한 후 재귀적으로 정렬, 두 배열을 병합하는 방식.
• 특징: 안정 정렬, 추가 메모리 필요.
• 시간 복잡도: $O(NlogN)$
• 파이썬 구현

def merge_sort(lst):
    if len(lst) <= 1:
        return lst
    mid = len(lst) // 2
    left = merge_sort(lst[:mid])
    right = merge_sort(lst[mid:])
    return merge(left, right)

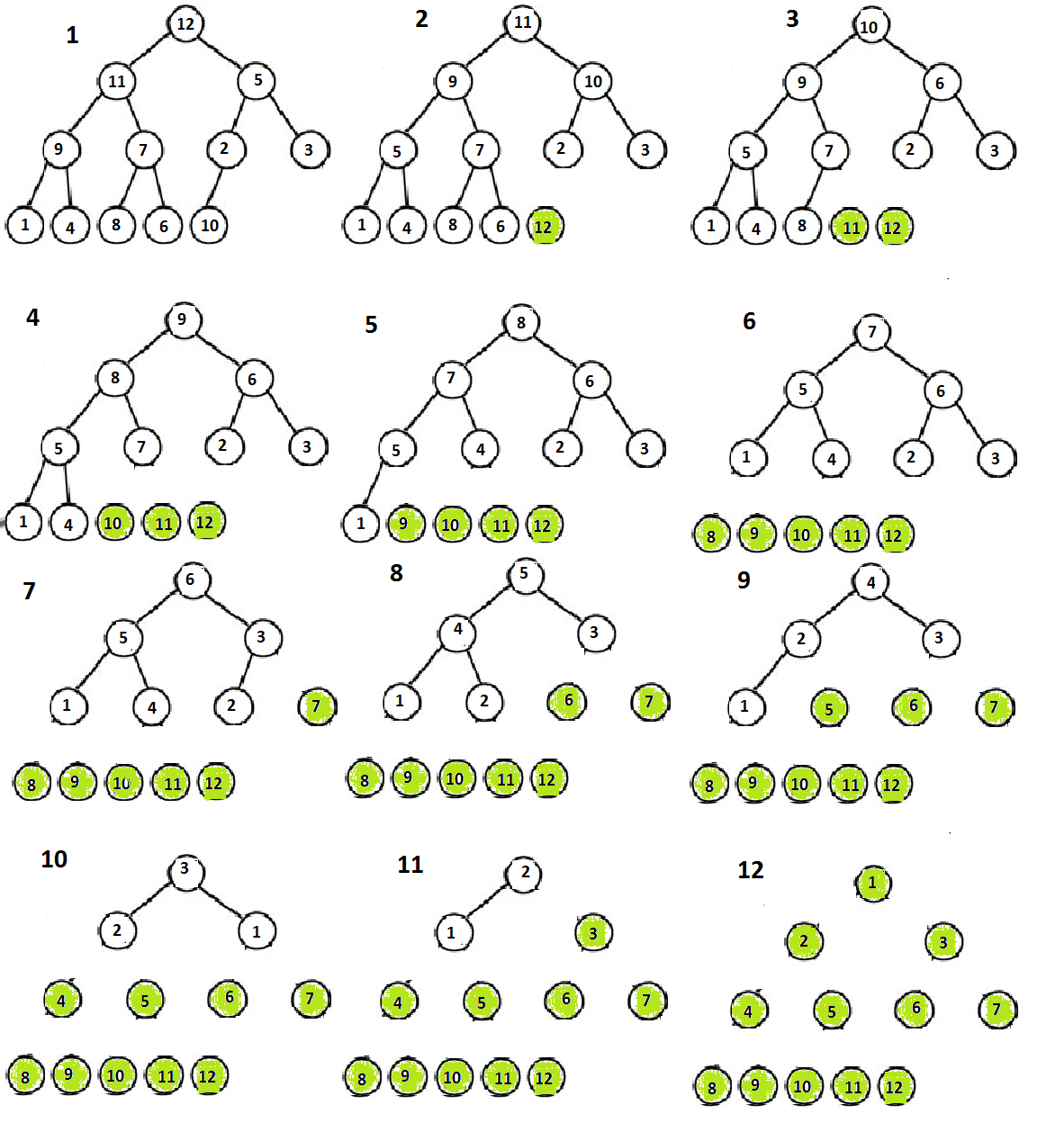
Heap Sort

• 주어진 배열을 최대 힙(또는 최소 힙)으로 구성한 후, 루트와 마지막 원소를 교환하며 정렬.
• 특징: in-place 정렬, 비교 기반 정렬.
• 시간 복잡도: $O(NlogN)$
• 파이썬 구현

def heapify(arr, index, heap_size):
    largest = index
    left = 2 * index + 1
    right = 2 * index + 2
    if left < heap_size and arr[left] > arr[largest]:
        largest = left
    if right < heap_size and arr[right] > arr[largest]:
        largest = right
    if largest != index:
        arr[index], arr[largest] = arr[largest], arr[index]
        heapify(arr, largest, heap_size)

def heap_sort(arr):
    n = len(arr)
    for i in range(n//2 - 1, -1, -1):
        heapify(arr, i, n)
    for i in range(n-1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        heapify(arr, 0, i)
    return arr

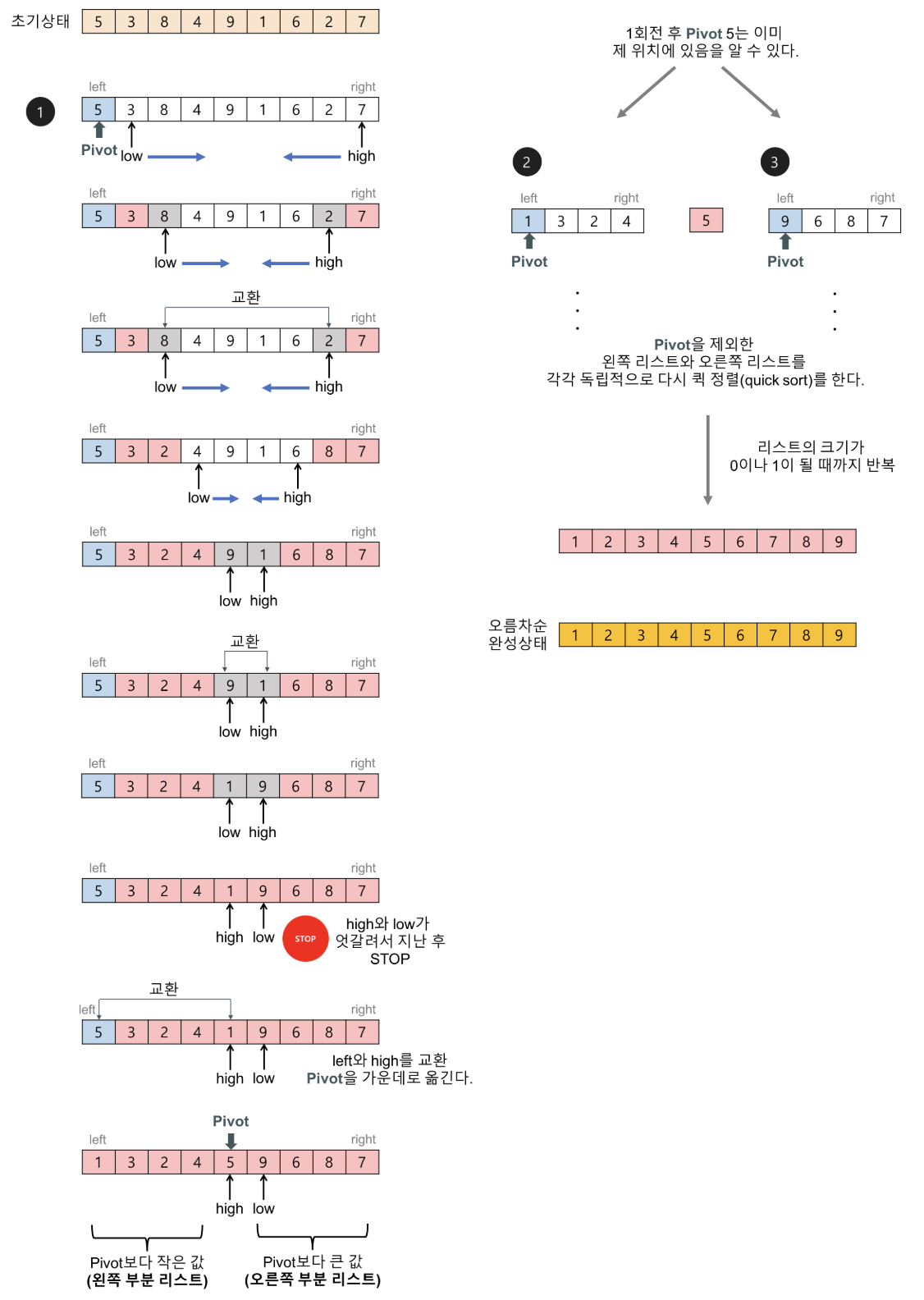
Quick Sort

• 기준(pivot)을 정해 pivot보다 작은 원소와 큰 원소로 분할하고, 분할된 배열에 대해 재귀적으로 정렬.
• 특징: 평균적으로 매우 빠르지만, pivot 선택에 따라 최악의 경우 O(N²) 발생 가능.
• 시간 복잡도:
  • 최악: $O(N²)$
  • 평균/최선: $O(NlogN)$
• 파이썬 구현

def quickSort(alist):
    quickSortHelper(alist, 0, len(alist)-1)

def quickSortHelper(alist, first, last):
    if first < last:
        splitpoint = partition(alist, first, last)
        quickSortHelper(alist, first, splitpoint-1)
        quickSortHelper(alist, splitpoint+1, last)

def partition(alist, first, last):
    pivotvalue = alist[first]
    leftmark = first + 1
    rightmark = last
    done = False
    while not done:
        while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
            leftmark += 1
        while rightmark >= leftmark and alist[rightmark] >= pivotvalue:
            rightmark -= 1
        if rightmark < leftmark:
            done = True
        else:
            alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
    alist[first], alist[rightmark] = alist[rightmark], alist[first]
    return rightmark

Divide and Conquer

• 개념: 큰 문제를 여러 개의 하위 문제로 분할한 후, 각 하위 문제를 독립적으로 해결하고 결과를 결합하는 방식.
• 예시: 재귀적 피보나치 계산

def fibb(n):
    if n <= 1:
        return 1
    return fibb(n-1) + fibb(n-2)

• 특징: 재귀 호출을 통한 문제 분할, 병합 단계가 중요한 역할.

Dynamic Programming

• 개념: 중복되는 하위 문제의 결과를 저장(메모이제이션 또는 타뷸레이션)하여 효율적으로 문제를 해결하는 방법.

• 하향식접근법 (Top-Down, 메모이제이션): 재귀 호출 중 이미 계산된 결과는 저장하여 재활용.

table = [None] * (n+1)
def fibb(n):
    if n <= 1:
        return 1
    if table[n] is not None:
        return table[n]
    table[n] = fibb(n-1) + fibb(n-2)
    return table[n]

• 상향식 (Bottom-Up, 타뷸레이션): 작은 문제부터 차례대로 계산하여 테이블에 저장.

def fibb(n):
    table = [1] * (n+1)
    for i in range(2, n+1):
        table[i] = table[i-1] + table[i-2]
    return table[n]

Greedy Algorithm

• 개념: 각 단계에서 지역적으로 최적의 선택을 하여 전체 문제의 최적해를 구하는 방식.
• 예시: 동전 거스름돈 문제 – 동전의 단위가 1, 5, 10원일 경우 그리디 선택이 가능하지만, 1, 7, 10원인 경우에는 최적해를 보장하지 않음.
• 주의점: 그리디 선택이 전체 최적해를 보장하는지 검증이 필요

Graph

• 개념: 정점(노드)과 간선(엣지)으로 구성된 자료구조.
• 활용: 경로 탐색, 최단 경로, 네트워크 연결 등 다양한 문제 해결에 사용됨.

Graph Traversal: BFS, DFS

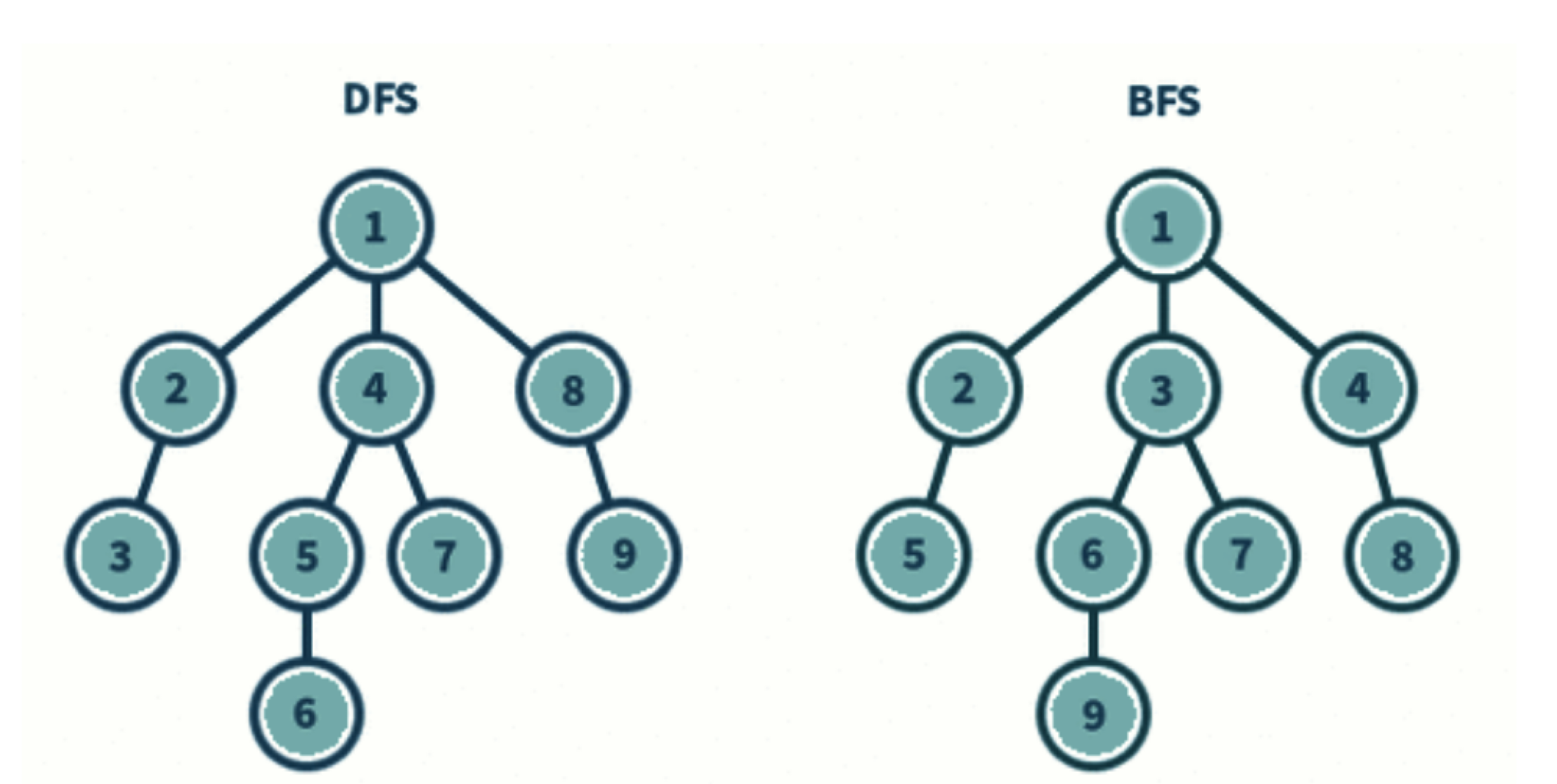
• BFS (너비 우선 탐색)
  • 방식: 시작 노드에서 인접한 노드를 먼저 방문하며, Queue를 사용.
  • 장점: 최단 경로 보장, 노드 수가 적고 깊이가 얕은 경우 빠름.
  • 단점: 메모리 사용량이 많아질 수 있음.
• DFS (깊이 우선 탐색)
  • 방식: 한 방향으로 깊게 탐색 후, 더 이상 진행할 수 없으면 이전 단계로 돌아감. 주로 Stack이나 재귀 사용.
  • 장점: 메모리 사용량이 비교적 적음, 구현이 간단함.
  • 단점: 최단 경로 보장이 어려움.
    

Shortest Path

• 개념: 그래프 내에서 한 노드에서 다른 노드로 가는 최단 경로(최소 비용 경로)를 찾는 문제.
• 알고리즘: Dijkstra, Floyd-Warshall, Bellman-Ford 등이 있음.

Dijkstra

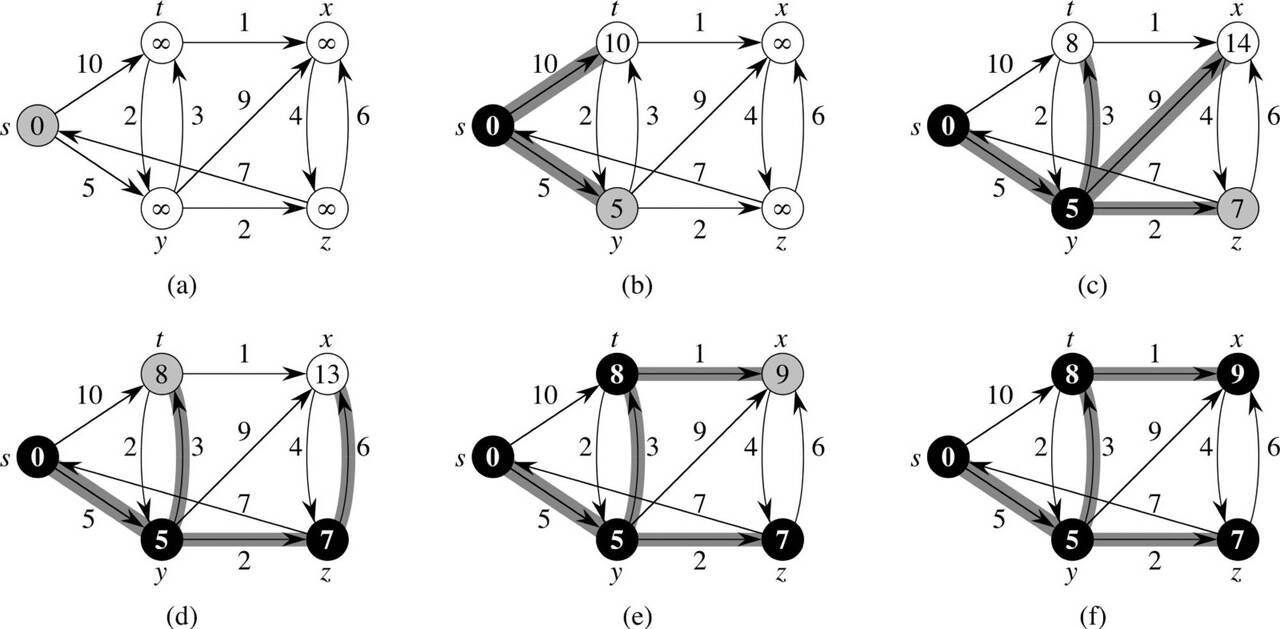
• 특징: 시작 노드에서 다른 모든 노드까지의 최단 거리를 구하며, 음수 가중치는 허용하지 않음.
• 동작 방식:
  • 시작 노드를 0, 나머지는 INF로 초기화.
  • 가장 짧은 거리를 가진 노드를 선택 후 인접 노드의 거리를 갱신.
  • 우선순위 큐를 사용하면 시간 복잡도 O(E log V) 달성 가능.
• 파이썬 구현 (핵심 부분)

import heapq
INF = int(1e9)

def dijkstra(start, graph, distance):
    q = []
    heapq.heappush(q, (0, start))
    distance[start] = 0
    while q:
        dist, now = heapq.heappop(q)
        if distance[now] < dist:
            continue
        for next_node, cost in graph[now]:
            new_cost = dist + cost
            if distance[next_node] > new_cost:
                distance[next_node] = new_cost
                heapq.heappush(q, (new_cost, next_node))

Floyd-Warshall

• 특징: 모든 정점 쌍에 대해 최단 경로를 구하는 알고리즘.
• 동작 방식:
  • 점화식: D[a][b] = min(D[a][b], D[a][k] + D[k][b])
  • 삼중 반복문을 사용하여 모든 중간 정점을 고려.
• 시간 복잡도: O(V³)
• 파이썬 구현 (핵심 부분)

for k in range(1, n+1):
    for i in range(1, n+1):
        for j in range(1, n+1):
            graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])

Bellman-Ford

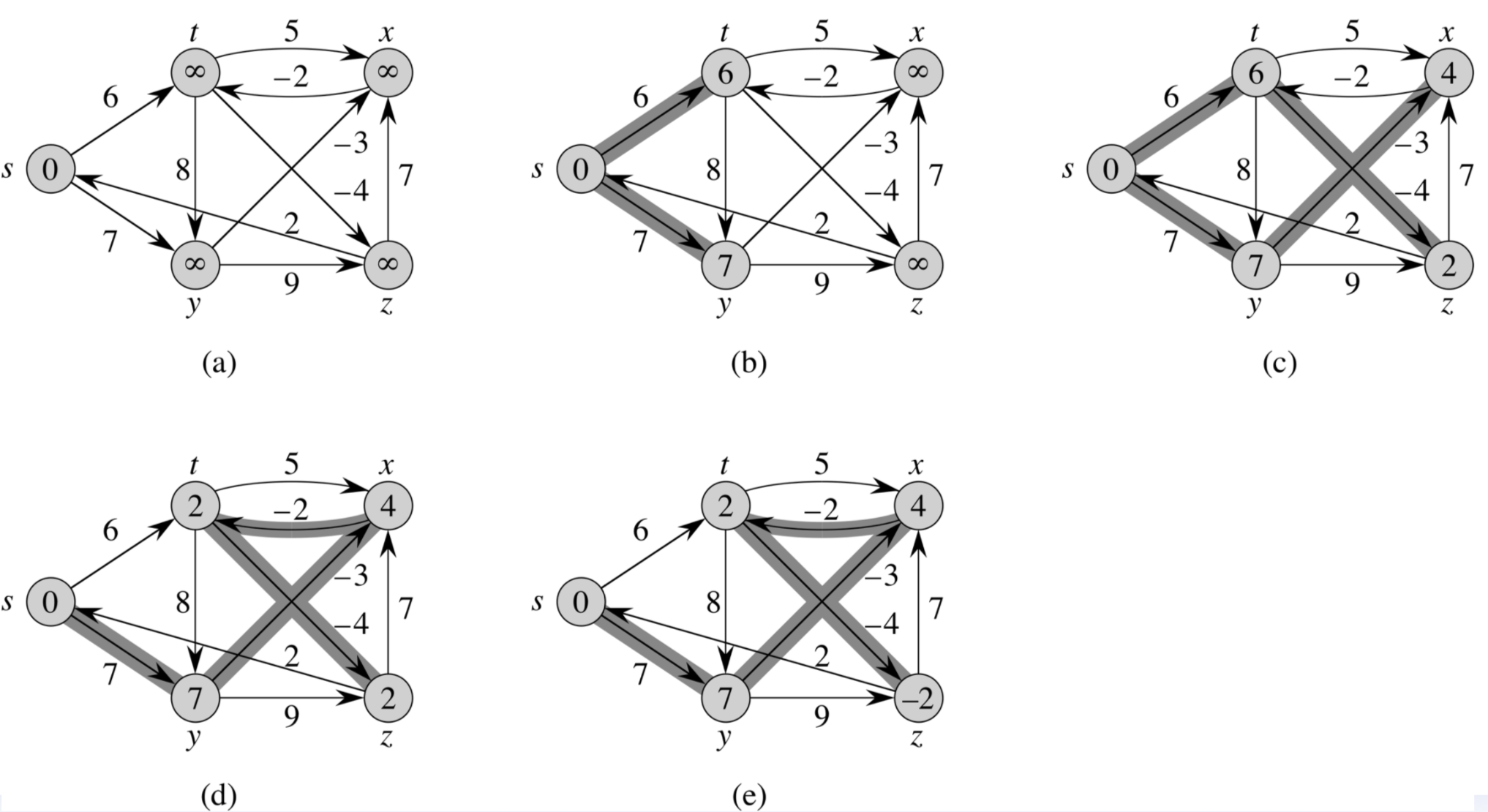
• 특징: 음수 가중지 간선이 있는 경우에도 최단 경로를 구하며, 음수 사이클 탐지가 가능함.
• 동작 방식:
  • 모든 간선을 V-1번 반복하며 최단 거리를 갱신.
  • 한 번 더 반복하여 갱신이 일어나면 음수 사이클 존재.
• 시간 복잡도: O(V × E)
• 파이썬 구현 (핵심 부분)

def bellman_ford(start, edges, dist, n):
    dist[start] = 0
    for i in range(n):
        for u, v, cost in edges:
            if dist[u] != INF and dist[v] > dist[u] + cost:
                dist[v] = dist[u] + cost
                if i == n - 1:
                    return True  # 음수 사이클 존재
    return False

Minimum Spanning Tree

• 개념: 모든 정점을 연결하면서 간선의 가중치 합이 최소인 트리.
• 알고리즘: Prim, Kruskal 등이 있음.

Prim

• 특징: 시작 정점에서부터 인접한 정점 중 최소 가중치 간선을 선택하며 MST를 확장.
• 시간 복잡도: 기본적으로 O(n²) (우선순위 큐 사용 시 개선 가능)
• 동작 방식:
  • 시작 정점을 MST에 포함.
  • 인접 노드 중 최소 비용의 노드를 선택 후 MST 확장.
    

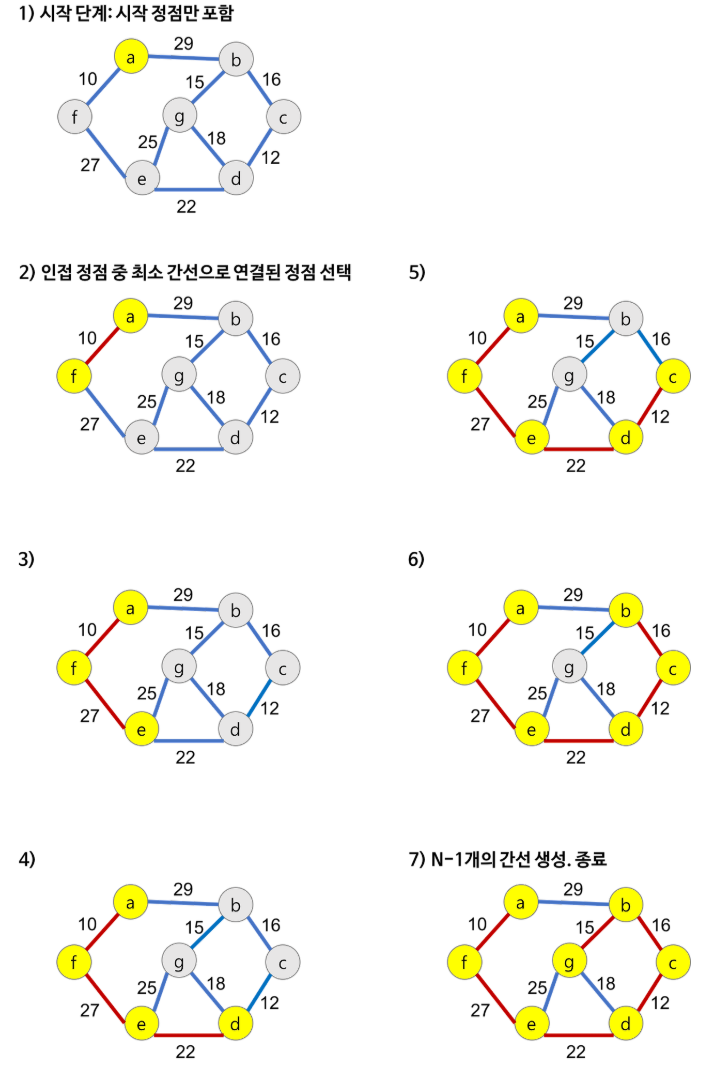
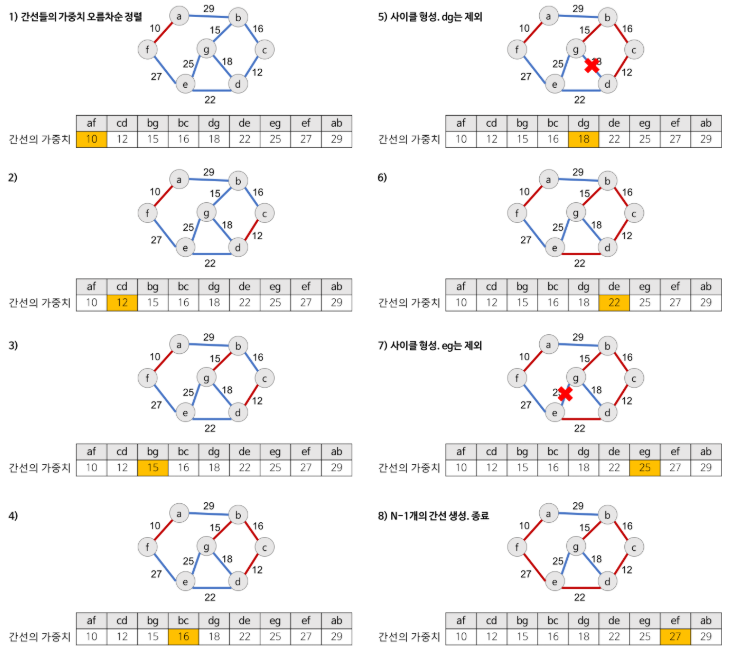
Kruskal

• 특징: 간선을 가중치 오름차순으로 정렬한 후, 사이클을 형성하지 않는 간선을 선택해 MST 구성.
• 시간 복잡도: O(e log e)
• 동작 방식:
  • 모든 간선을 정렬.
  • Union-Find 자료구조를 사용해 사이클 여부를 판별하며 간선 선택.